Matrice, Quaternion et graphe de scène – Partie 1
Bonjour à tous, aujourd’hui on va parler mathématiques appliqués si possible de manière simple car on va parler de matrice & quaternion.
Le but de ces articles est de correctement les utiliser dans un graphe de scène et notamment pour le calcul de la “modelview-projection”.
Avant de commencer
Je vais avoir une approche beaucoup plus ludique que mathématiques. Les informations exposées ne sont malheureusement pas toutes tirées de sources fiables certaines viennent de mon expérience propre :
N’hésitez pas à m’apporter d’autres sources dans les commentaires.
Code source
J’utiliserai la bibliothèque glm pour manipuler les matrices et quaternions. C’est gratuit, c’est que des .h (pas .lib ni .dll), c’est cross-platform.
Pour finir avec le code, j’utilise les macros EXPECT_EQ et autres de Google Test.
Tous les exemples sont sur mon GitHub https://github.com/Rominitch/myBlogSource/ dans Matrix_Quaternion.
Notation
Dans les exemples, on va utiliser la convention d’écriture suivante:
- Multiplication de droite à gauche
- Matrice en ligne (ou row-major en anglais)
Notation simple
Notation étendue
![Rendered by QuickLaTeX.com \begin{align*} & {\color{myR}\begin{bmatrix} m_{0} & m_{1} & m_{2} & m_{3} \\ m_{4} & m_{5} & m_{6} & m_{7} \\ m_{8} & m_{9} & m_{10} & m_{11} \\ m_{12} & m_{13} & m_{14} & m_{15} \end{bmatrix}} \\ {\color{myG} \begin{bmatrix} v_{0} & v_{1} & v_{2} & v_{3} \end{bmatrix}} & \mspace{5mu} \bigl[ {\color{myB}\begin{matrix} \makebox[\widthof{$m_{12}$}]{$r_{0}$} & \makebox[\widthof{$m_{13}$}]{$r_{1}$} & \makebox[\widthof{$m_{14}$}]{$r_{2}$} & \makebox[\widthof{$m_{15}$}]{$r_{3}$} \end{matrix}} \mspace{5mu} \bigr] \end{align*}](https://mouca.fr/wordpress/wp-content/ql-cache/quicklatex.com-a8c9165bc15fab1c2fe6e24298897ece_l3.png)
Code source équivalent
glm::mat4 matrix(0.0f, 1.0f, 0.0f, 0.0f,
1.0f, 0.0f, 0.0f, 0.0f,
0.0f, 0.0f, 1.0f, 0.0f,
0.0f, 0.0f, 0.0f, 1.0f);
glm::vec4 vector(2.0f, 3.0f, 4.0f, 1.0f);
glm::vec4 result = matrix * vector;
Les indices 0,1,2,3, … désignent aussi l’adresse mémoire de chaque case.
Et donc on va s’autoriser à écrire: ![]()
glm::mat4 m(0.5f, 0.0f, 0.0f, 0.0f,
0.0f, 0.5f, 0.0f, 0.0f,
0.0f, 0.0f, 0.5f, 0.0f,
0.0f, 0.0f, 0.0f, 1.0f);
glm::mat4 v(0.0f, 1.0f, 0.0f, 0.0f,
1.0f, 0.0f, 0.0f, 0.0f,
0.0f, 0.0f, 1.0f, 0.0f,
0.0f, 0.0f, 0.0f, 1.0f);
glm::mat4 p(1.0f, 0.0f, 0.0f, 0.0f,
0.0f, 1.0f, 0.0f, 0.0f,
0.0f, 0.0f, 1.0f, 0.0f,
1.0f, 2.0f, 3.0f, 1.0f);
glm::mat4 result = p * (v * m);
glm::mat4 mvp(0.0f, 0.5f, 0.0f, 0.0f,
0.5f, 0.0f, 0.0f, 0.0f,
0.0f, 0.0f, 0.5f, 0.0f,
1.0f, 2.0f, 3.0f, 1.0f);
EXPECT_EQ(mvp, result);
EXPECT_NE(mvp, m * v * p);
Je ne sais pas si c’est une “vraie” convention d’écriture mais en tout cas elle est très proche du code.
Pour des raisons de simplification et avoir des schémas faciles à lire, on va travailler dans le plan Z=0.
On reste bien en 3D dans notre logique et nos formules.
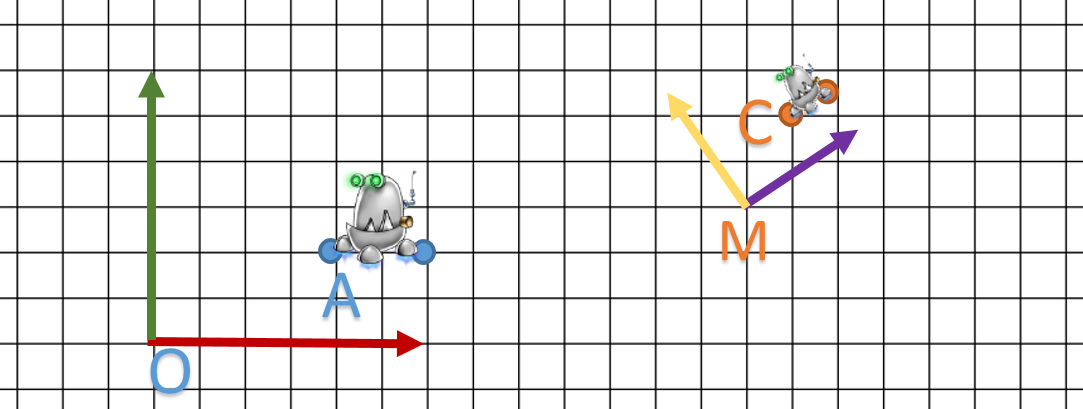
J’ai mon repère orthonormé O avec son axe X et son axe Y, Z étant vers nous.
Les unités dépendent des longueurs des vecteurs x et y.
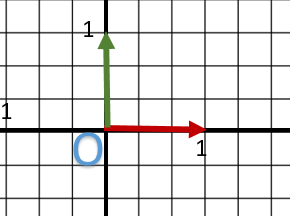
Bref c’est du classique.
Les Matrices
Les matrices de transformation homogènes (que l’on nommera matrice par la suite) nous permet d’appliquer une transformation géométrique (plus ou moins complexe) à un vecteur ou point.
Je vais partir du principe que vous savez les manipuler (en gros faire l’ addition/multiplication/transposé/inversion) ou que votre programme/bibliothèque sait très bien le faire pour vous !
Rappel: les principales formes
Voici les principales formes de matrice de transformation qu’on utilise.
La translation T
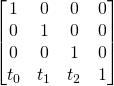
La rotation R
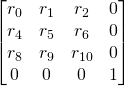
L’homothétie S
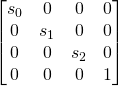
Problème 1: Qu’est-ce qu’une matrice de transformation ? et comment les forme-t-on ?
Translation et représentation de ce qu’est une matrice
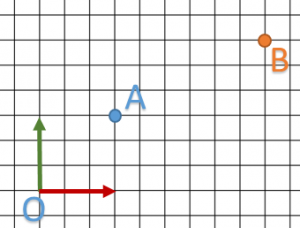
On va prendre une approche naïve du problème. Pour commencer, on va utiliser les matrices pour translater notre point.
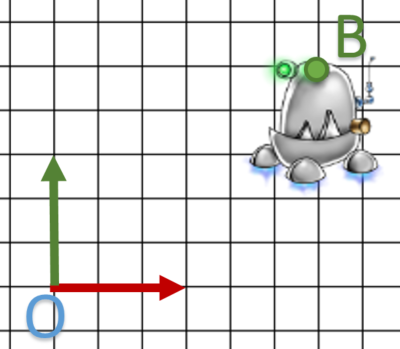
J’ai le schéma suivant: je veux déplacer mon point A vers le point B.
On lit facilement ![]() et
et ![]() donc le vecteur de translation est
donc le vecteur de translation est ![]() .
.
On va substituer les valeurs “t” de notre matrice par ce vecteur et calcul la multiplication avec A.
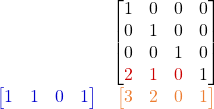
glm::vec4 b( 3.0f, 2.0f, 0.0f, 1.0f);
glm::vec4 a( 1.0f, 1.0f, 0.0f, 1.0f);
glm::mat4 t( 1.0f, 0.0f, 0.0f, 0.0f,
0.0f, 1.0f, 0.0f, 0.0f,
0.0f, 0.0f, 1.0f, 0.0f,
2.0f, 1.0f, 0.0f, 1.0f );
EXPECT_EQ( b, t * a );
glm::mat4 t2( 1.0f ); // Identity
t2 = glm::translate( t2, glm::vec3( 2.0f, 1.0f, 0.0f ) );
EXPECT_EQ( b, t2 * a );
Donc on retrouve bien notre point B.
- Ça marche mais bon qu’est-ce qui s’est vraiment passé ?
- C’est vachement plus compliqué que d’appliquer un vecteur de translation ?
- A quoi ont servi les autres parties de la matrice ?
Alors c’est là que les choses se compliquent car en fait on a pas vraiment appliquer un vecteur de translation. Il faut voir cette opération comme un changement de point de vue. Notre objet n’a pas été changé mais c’est plutôt là où on le regarde.
Mathématiquement, les matrices nous permettent de faire un changement de repère (base).
Leur forme est la suivante:
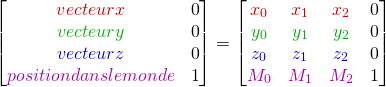
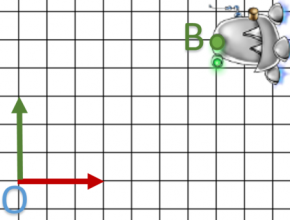
Voici le “vrai” schéma de ce qui c’est passé: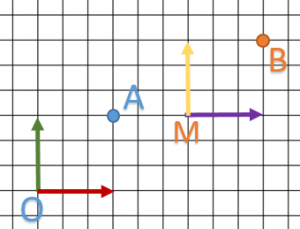
Donc notre matrice de translation va créer un autre repère M qui a trois vecteurs x,y,z identiques au premier. On remarque que :
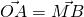 donc le dessin initiale (ici juste un point) ne bouge pas par rapport au repère.
donc le dessin initiale (ici juste un point) ne bouge pas par rapport au repère.- B est exprimé dans le repère
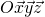 .
.
Mais il reste un dernier point important a expliqué : Si B est exprimé dans le repère O, A est exprimé dans quel repère ?
La réponse est : dans le repère M.
J’appelle repère ![]() , le repère définit par une origine X et sa base
, le repère définit par une origine X et sa base ![]() .
.
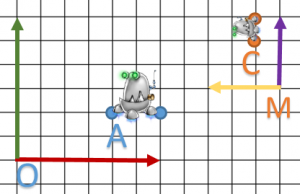
- J’ai un objet 3D : un robot sous un logiciel de modélisation (exemple: Blender).
Il a son propre repère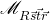 et un point
et un point 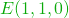 pour son œil.
pour son œil.
- Je vais l’utiliser dans mon programme qui a le repère
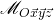 . Et un autre repère
. Et un autre repère 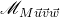 qui dépends du monde O car le point M est défini dans O.
qui dépends du monde O car le point M est défini dans O.
- Si je dessine mon objet sur O ou sur M (en adaptant le repère
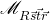 ), je vais transformer mon point E soit en A ou B pour le repère O.
), je vais transformer mon point E soit en A ou B pour le repère O.
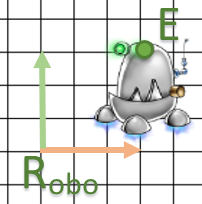
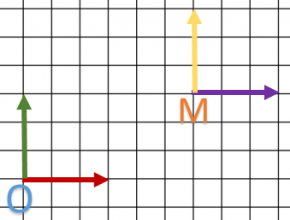
Finalement, on a définit deux repères O et M. Le point A est exprimé dans le repère M et B dans le repère O. Notre matrice fait une transformation du repère M vers O.
Le repère O va s’appeler le repère supérieur de M car M est défini par rapport à O : on a une notion de hiérarchie.
On vient d’ajouter une notion importante à notre matrice: son sens d’application.
Pour changer de sens, il faut tout simplement appliquer une inversion de matrice car les matrices de transformation précédentes sont toutes inversibles.
Pour conclure :
- Une matrice représente un changement de base entre repère local et le repère supérieur.
- Elle a un sens d’application: repère supérieur vers local ou inversement.
Pour la suite, on va donc former nos matrices dans le sens: locale vers repère supérieur car elles sont beaucoup plus facile à former.
En anglais, on parle de Global/World et Local (coordinate).
La rotation
La matrice de rotation va donc nous permettre de définir la base de notre système. On va utiliser des vecteurs normalisés.
La forme de la matrice est la suivante:
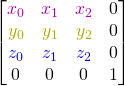
Il est facile par exemple d’écrire la matrice de rotation de ![]() par rapport à
par rapport à ![]() .
.
On part du schéma suivant :
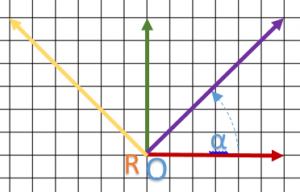
On peut facilement lire que ![]() ,
, ![]() et
et ![]() .
.
Je pose ![]() soit
soit ![]() cela va me permettre de normaliser mes vecteurs. En fait,
cela va me permettre de normaliser mes vecteurs. En fait, ![]() .
.
Pour ceux qui connaissent par cœur leur matrice de rotation autour de ![]() , les sin() et cos() sont bien présents.
, les sin() et cos() sont bien présents.
En normalisant chacun des vecteurs et remplaçant, on trouve la matrice
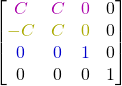
const float pi_4 = 0.785398163397448309616f;
const float C = 1.0f / sqrt(2.0f);
// Matrice manuelle
glm::mat4 r( C, C, 0.0f, 0.0f,
-C, C, 0.0f, 0.0f,
0.0f, 0.0f, 1.0f, 0.0f,
0.0f, 0.0f, 0.0f, 1.0f);
// En utilisant l'API glm
glm::mat4 r1(1.0f); // Identity
r1 = glm::rotate(r1, pi_4, glm::vec3(0.0f, 0.0f, 1.0f));
EXPECT_EQ(r, r1);
Appliquons la matrice sur cette exemple: ![]() et
et ![]() (c’est assez facile à calculer juste avec le théorème de Pythagore et en remarquant que OA = coordonnée y de B)
(c’est assez facile à calculer juste avec le théorème de Pythagore et en remarquant que OA = coordonnée y de B)
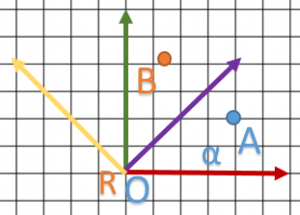
![Rendered by QuickLaTeX.com \begin{align*} & \begin{bmatrix} {\color{myM} C} & {\color{myM}C} & {\color{myM}0} & 0 \\ {\color{myY}-C} & {\color{myY}C} & {\color{myY}0} & 0 \\ {\color{myB} 0} & {\color{myB}0} & {\color{myB}1} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \\ {\color{myR}\begin{bmatrix}\frac{2}{3} & \frac{1}{3} & 0 & 1\end{bmatrix}} & \mspace{5mu} \bigl[ {\color{myB}\begin{matrix} \makebox[\widthof{$-C$}]{$\frac{C}{3}$} & \makebox[\widthof{$C$}]{$C$} & \makebox[\widthof{$0$}]{0} & \makebox[\widthof{$1$}]{1} \end{matrix}} \mspace{5mu} \bigr] \end{align*}](https://mouca.fr/wordpress/wp-content/ql-cache/quicklatex.com-cead821fc733039de081a10ed4a03e55_l3.png)
const float C = 1.0f / sqrt(2.0f);
glm::mat4 r( C, C, 0.0f, 0.0f,
-C, C, 0.0f, 0.0f,
0.0f, 0.0f, 1.0f, 0.0f,
0.0f, 0.0f, 0.0f, 1.0f);
glm::vec4 a(2.0f/3.0f, 1.0f/3.0f, 0.0f, 1.0f);
glm::vec4 b( C/3.0f, C, 0.0f, 1.0f);
EXPECT_EQ(b, r * a);
Cool ! C’est exactement le bon résultat.
Pour conclure :
- On tourne autour de l’origine R
- On peut “facilement” vérifier qu’une matrice est correcte (en regardant si le vecteur est positif/négatif sur chacun des composantes).
- B est exprimé dans le repère
 .
.
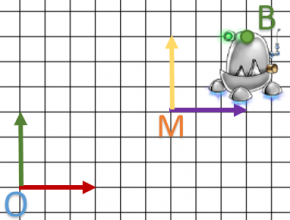
Sur un modèle complexe, la rotation donnera la représentation suivante:
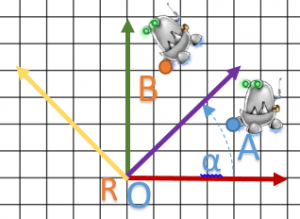
Une nouvelle question s’offre à nous : comment tourner autour d’un autre point ? Hum … On verra cela en fin d’article.
Et pour finir l’homothétie
Finissons notre tour des matrices avec l’homothétie. Ici, la forme est facile à comprendre on va “étirer” notre objet sur chaque dimension.
Chaque facteur d’agrandissement est défini dans l’ensemble ![]() .
.
Quand il est supérieur 1 : on agrandie, et entre 0 et 1 : on réduit.
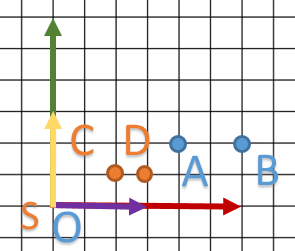
Dans l’exemple suivant, on va réduire notre repère par deux sur toutes les dimensions.
Cette fois-ci, on va prendre deux points afin de mieux comprendre le phénomène.
- A deviendra C
- B deviendra D
glm::vec3 h(0.5f, 0.5f, 0.5f);
glm::mat4 m(h.x, 0.0f, 0.0f, 0.0f,
0.0f, h.y, 0.0f, 0.0f,
0.0f, 0.0f, h.z, 0.0f,
0.0f, 0.0f, 0.0f, 1.0f);
glm::mat4 m1(1.0f); // Identity
m1 = glm::scale(m1, h);
EXPECT_EQ(m1, m);
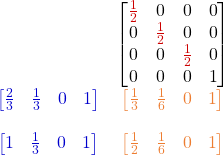
glm::vec4 a(2.0f/3.0f, 1.0f/3.0f, 0.0f, 1.0f);
glm::vec4 b(1.0f, 1.0f/3.0f, 0.0f, 1.0f);
glm::vec4 c(1.0f/3.0f, 1.0f/6.0f, 0.0f, 1.0f);
glm::vec4 d(1.0f/2.0f, 1.0f/6.0f, 0.0f, 1.0f);
EXPECT_EQ(c, m * a);
EXPECT_EQ(d, m * b);
Finalement voici l’effet sur notre petit robot.
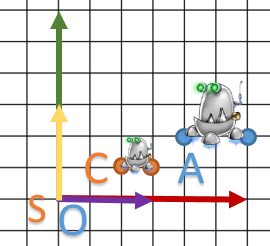
Voici quelques remarques:
- C et D est exprimé dans le repère
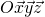 .
. - Notre robot n’a pas bougé par rapport à son repère: le point C est toujours à
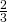 du vecteur et le point D est à l’extrémité du vecteur.
du vecteur et le point D est à l’extrémité du vecteur.
En conclusion de cette première partie, on a pu voir que la formation des matrices reste facile même si la rotation demande quelques calculs mais cela reste analysable (lors de vos phases de debug).
Problème 2: La composition
Généralement, ce qui va nous intéresser c’est de les composer afin de transformer nos points/vecteurs le plus rapidement possible (soit le moins d’opération processeur possible).
Petit rappel important:
LE PRODUIT MATRICIEL N’EST PAS COMMUTATIVE SOIT ![]() !
!
Donc l’ordre des opérations est super important mais la règle est simple :
Par simplification d’écriture, je vais appeler ces matrices composées: matrices HRT.
On va quand même prendre un exemple pour se le prouver.
On va dans un premier temps calculer la composée:
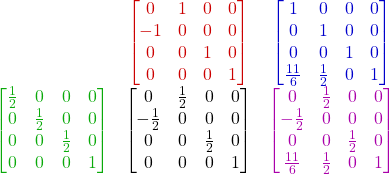
const float PI = 3.14159265358979323846f;
glm::mat4 s = glm::scale(glm::mat4(1.0f), glm::vec3(0.5f, 0.5f, 0.5f));
glm::mat4 r = glm::rotate(glm::mat4(1.0f), PI*0.5f, glm::vec3(0.0f, 0.0f, 1.0f));
glm::mat4 t = glm::translate(glm::mat4(1.0f), glm::vec3(11.0f/6.0f, 0.5f, 0.0f));
glm::mat4 m(0.0f, 0.5f, 0.0f, 0.0f,
-0.5f, 0.0f, 0.0f, 0.0f,
0.0f, 0.0f, 0.5f, 0.0f,
11.0f/6.0f, 0.5f, 0.0f, 1.0f);
glm::mat4 c = t * r * s;
// Near expected
for(int rawID=0; rawID < 4; ++rawID)
{
for(int columnID=0; columnID < 4; ++columnID)
{
EXPECT_NEAR(m[rawID][columnID], c[rawID][columnID], 1e-6f);
}
}
Si on applique cette nouvelle matrice sur le point ![]() .
.
![Rendered by QuickLaTeX.com \begin{align*} & \color{myM}{\begin{bmatrix} 0 & \frac{1}{2} & 0 & 0 \\ -\frac{1}{2} & 0 & 0 & 0 \\ 0 & 0 & \frac{1}{2} & 0 \\ \frac{11}{6} & \frac{1}{2} & 0 & 1 \end{bmatrix} } \\ {\color{myR}\begin{bmatrix}\frac{2}{3} & \frac{1}{3} & 0 & 1\end{bmatrix}} & \mspace{5mu} \bigl[ {\color{myB}\begin{matrix} \makebox[\widthof{$-\frac{1}{2}$}]{$\frac{5}{3}$} & \makebox[\widthof{$\frac{1}{2}$}]{$\frac{5}{6}$} & \makebox[\widthof{$0$}]{0} & \makebox[\widthof{$1$}]{1} \end{matrix}} \mspace{5mu} \bigr] \end{align*}](https://mouca.fr/wordpress/wp-content/ql-cache/quicklatex.com-674feac095ed76d93efc299c89cf8c99_l3.png)
glm::mat4 m(0.0f, 0.5f, 0.0f, 0.0f,
-0.5f, 0.0f, 0.0f, 0.0f,
0.0f, 0.0f, 0.5f, 0.0f,
11.0f/6.0f, 0.5f, 0.0f, 1.0f);
glm::vec4 a(2.0f/3.0f, 1.0f/3.0f, 0.0f, 1.0f);
glm::vec4 b(5.0f/3.0f, 5.0f/6.0f, 0.0f, 1.0f);
glm::vec4 mul = m * a;
// Near expected
for(int columnID=0; columnID < 4; ++columnID)
{
EXPECT_NEAR(b[columnID], mul[columnID], 1e-6f);
}
Rotation autour d’un autre point
Comme on l’a vu précédemment, la matrice de rotation tourne autour de l’origine de notre repère. Mais on veux souvent tourner autour d’un autre point: voici la méthodologie simple.
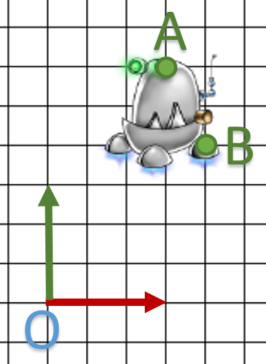
- Soit le modèle suivant; on veux tourner autour de B.
- On translate B sur l’origine du repère local soit
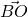 .
.
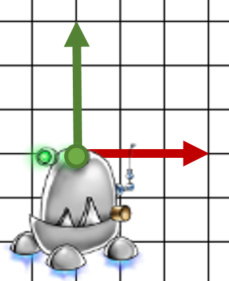
3. On applique la matrice de rotation.
- On applique la translation opposé soit
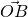 .
.
Au final, la transformation se traduit par: une translation + une rotation + une translation.
Mais on a vu que la composition permet de former une matrice HRT mais peut-on en combiner plusieurs ?
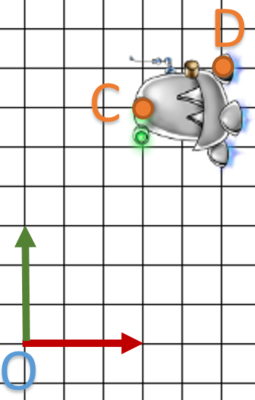
On va chercher à voir par l’exemple si la composition de cette matrice existe:![]()
On va partir de cet exemple: ![]() et
et ![]() des points de l’objet, on souhaite appliquer une rotation de
des points de l’objet, on souhaite appliquer une rotation de ![]() autour de A.
autour de A.
Ce qui va nous donner les points ![]() et
et ![]()
C’est parti :
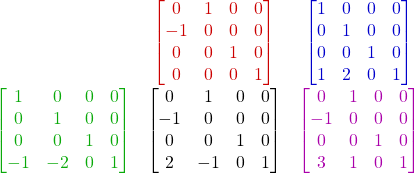
const float PI = 3.14159265358979323846f;
glm::mat4 m( 0.0f, 1.0f, 0.0f, 0.0f,
-1.0f, 0.0f, 0.0f, 0.0f,
0.0f, 0.0f, 1.0f, 0.0f,
3.0f, 1.0f, 0.0f, 1.0f );
glm::mat4 op = glm::translate( glm::mat4( 1.0f ), glm::vec3( 1.0f, 2.0f, 0.0f ) );
glm::mat4 po = glm::inverse( op );
glm::mat4 r = glm::rotate( glm::mat4( 1.0f ), PI*0.5f, glm::vec3( 0.0f, 0.0f, 1.0f ) );
glm::mat4 c = op * r * po;
// Near expected
for( int rawID=0; rawID < 4; ++rawID )
{
for( int columnID=0; columnID < 4; ++columnID )
{
EXPECT_NEAR( m[rawID][columnID], c[rawID][columnID], 1e-6f );
}
}
Et maintenant, on l’applique à nos points
![Rendered by QuickLaTeX.com \begin{align*} & {\color{myM}\begin{bmatrix} 0 & 1 & 0 & 0 \\ -1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 3 & 1 & 0 & 1 \end{bmatrix}} \\ {\color{myG} \begin{bmatrix} \frac{4}{3} & \frac{4}{3} & 0 & 1 \end{bmatrix}} & \mspace{5mu} {\color{myO} \bigl[\begin{matrix} \makebox[\widthof{$-1$}]{$\frac{5}{3}$} & \makebox[\widthof{$1$}]{$\frac{7}{3}$} & \makebox[\widthof{$0$}]{$0$} & \makebox[\widthof{$0$}]{$1$} \end{matrix} \mspace{5mu} \bigr]} \end{align*}](https://mouca.fr/wordpress/wp-content/ql-cache/quicklatex.com-8d8096574190e041787a98bfa411e3bb_l3.png)
glm::mat4 m( 0.0f, 1.0f, 0.0f, 0.0f,
-1.0f, 0.0f, 0.0f, 0.0f,
0.0f, 0.0f, 1.0f, 0.0f,
3.0f, 1.0f, 0.0f, 1.0f );
glm::vec4 a( 1.0f, 2.0f, 0.0f, 1.0f );
glm::vec4 b( 4.0f/3.0f, 4.0f/3.0f, 0.0f, 1.0f );
glm::vec4 c( 1.0f, 2.0f, 0.0f, 1.0f ); glm::vec4 d( 5.0f/3.0f, 7.0f/3.0f, 0.0f, 1.0f );
EXPECT_EQ( c, m * a );
glm::vec4 computed = m * b;
// Near expected
for( int columnID=0; columnID < 4; ++columnID )
{
EXPECT_NEAR( d[columnID], computed[columnID], 1e-6f );
}
Je vous laisse faire le calcul pour C et vous verrez qu’on retrouve bien A et inversement.
Cette solution est facile à comprendre et assez intuitive et en plus elle se fait en une seule multiplication matricielle.
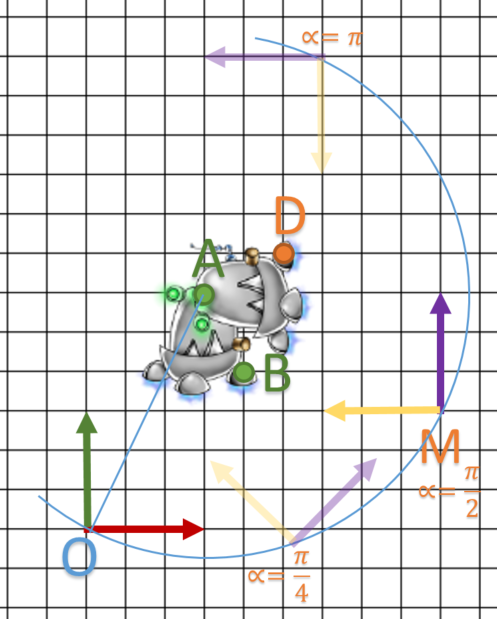
Pour info, un dernier petit schéma:
Finalement, on conclue que nos matrices HRT peuvent être cumuler et mis en cascade : c’est ce point qui nous sera très utile lors de leur utilisation dans le graphe de scène.
Conclusion
On a vu :
- Une définition des matrices homogènes de transformation
- Leurs principales formes et comment les former
- Leurs compositions
A ce stade, on a tous les outils pour utiliser nos matrices dans un graphe de scène.
Mais avant, je souhaiterai passer aux quaternions : Matrice, Quaternion et graphe de scène – Partie 2
Si à ce stade les quaternions ne vous branchent pas : Matrice, Quaternion et graphe de scène – Partie 3
Merci d’avoir lu cet article !
N’hésitez pas à le partager, à me signaler les problèmes, et aussi commenter afin d’en faire un outils dynamique et constructif !
Sources
Wikipedia : Produit matriciel
Wikipedia : Transformation matrix
Wikipedia : Matrice de passage
www.opengl-tutorial.org – Tutorial 3 : Matrices
Les transformations géométriques du plan
University of Edinburgh – Transformations – Taku Komura