Matrice, Quaternion et graphe de scène – Partie 3
Nous allons terminer notre compréhension des matrices et quaternions avec un exemple concret : l’utilisation de ces outils dans un graphe de scène.
On va apprendre à manipuler la hiérarchie des objets et calculer la modèle-vue (ou ModelView en anglais).
Cette article s’inscrit dans une suite :
- Matrice, Quaternion et graphe de scène – Partie 1
- Matrice, Quaternion et graphe de scène – Partie 2
- Matrice, Quaternion et graphe de scène – Partie 3
On a vu précédemment plusieurs manières de manipuler le positionnement de nos objets grâce aux matrices, aux structures de transformation (basé sur les quaternions).
Notre objectif est maintenant d’utiliser la composition de nos outils afin de donner des instruction à notre ordinateur pour dessiner des objets.
Vocabulaire
Beaucoup de termes qui vont suivre sont des traductions de termes anglais.
Je vais essayer d’en donner des traductions françaises, les plus proches à mon sens, du sens premier du mot anglais.
Je vais aussi introduire des termes personnels qui selon moi décrivent mieux les notions/outils.
On va commencer par la Transformation qui est la représentation des trois transformations (rotation, translation et homothétie) en une seule structure. Ça peut être une matrice 4×4 ou la structure du même nom vue dans la partie 2.
Graphe de scène
Le graphe de scène est une forme de représentation d’une scène 3D sous forme de graphe. Chaque élément de la scène est représenté dans un nœud et les liaisons permettent de mettre en relation les nœuds et ainsi de définir une hiérarchie.
Le but est de créer un graphe le plus simple possible avec les meilleures relations.
On appelle généralement “root” ou “world” le nœud le plus haut qui a pour but de contenir toute la scène.
Ensuite, on y trouve des nœuds finaux ou intermédiaires :
- Dans les nœuds finaux, on trouve les sources de lumière, les objets à afficher, …
- Dans les nœuds intermédiaires, on trouve la “transformation”, des propriétés graphiques, …
Bien sur, les types de nœuds, leurs statuts finaux ou non dépendent fortement de celui qui conçoit le graphe. Il n’y a pas réellement de “standard” mais juste des bonnes pratiques.
Voici à quoi ça peut ressembler :
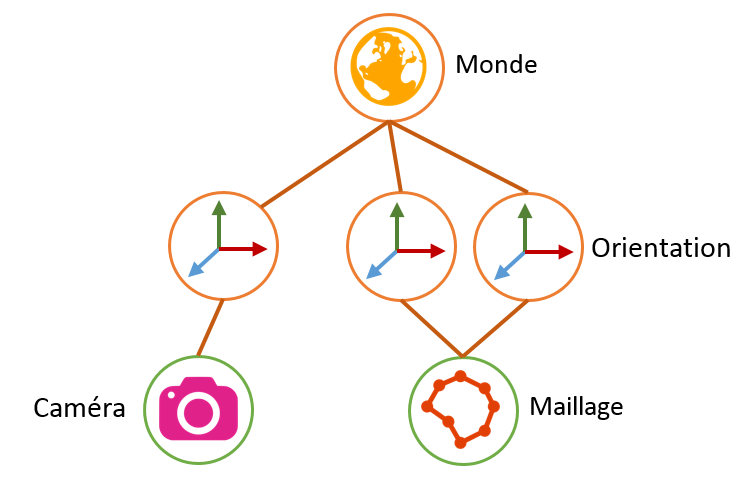
On va parler d’un graphe de scène purement dans le placement des objets de notre scène. On va se focaliser sur trois types de nœuds:
- La transformation: ce dont on parle depuis le début.
- La camera: dans sa forme la plus simple, c’est à dire la matrice de projection.
- Le maillage(mesh): notre soupe de points.
Le graphe de scène : construction
On va illustrer tout ce qu’on a vu avec un exemple. Afin de rester simple, on va se focaliser sur les homothéties et les translation.
Voici la scène suivante:

Une vallée avec un chemin de fer. Sur les rails, j’ai un train et sur mon train, j’ai un personnage qui marche. La camera filme mon personnage et se déplace derrière lui.
On va dans un premier temps modéliser notre graphe.
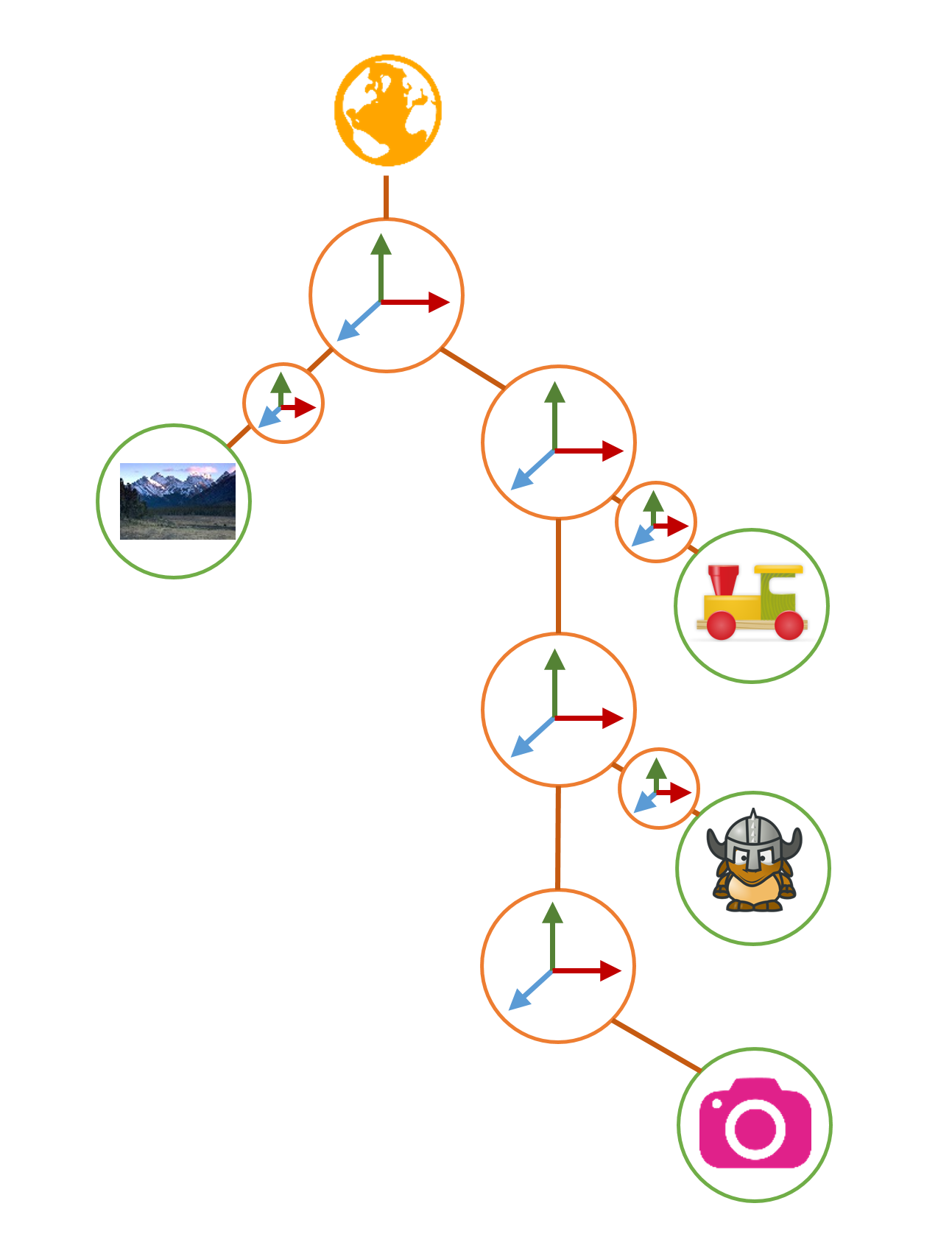
J’ai volontairement mis pleins de nœuds transformations, on se posera la question de leur utilité plus tard.
Maintenant, nous allons préparer nos maillages. Nous allons charger les données suivantes :
La vallée
Le train
Le personnage

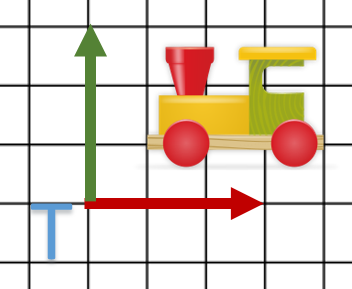
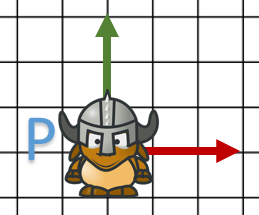
Comme on peut le voir, les données ne sont pas dans les mêmes unités et leurs positions/homothéties doivent être changées.
Si j’importe tout dans mon programme, en respectant la hiérarchie établie et, en utilisant des “transformations identités”, j’obtiens le résultat suivant :

Ce n’est pas vraiment le résultat attendu.
On va calculer les transformations de chacun de nos modèles. L’idée est de changer la position du modèle et son homothétie afin de mieux la manipuler plus tard :
- On va définir le nouveau centre de nos objets “train” et “personnage” comme étant le point centrée en bas de l’objet.
- Pour l’homothétie, on va équilibrer chaque maillage par rapport à la vallée
On se retrouve avec les transformations suivantes :
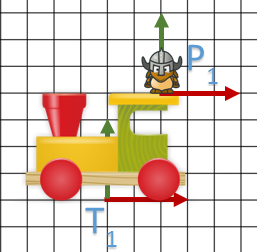
Le train
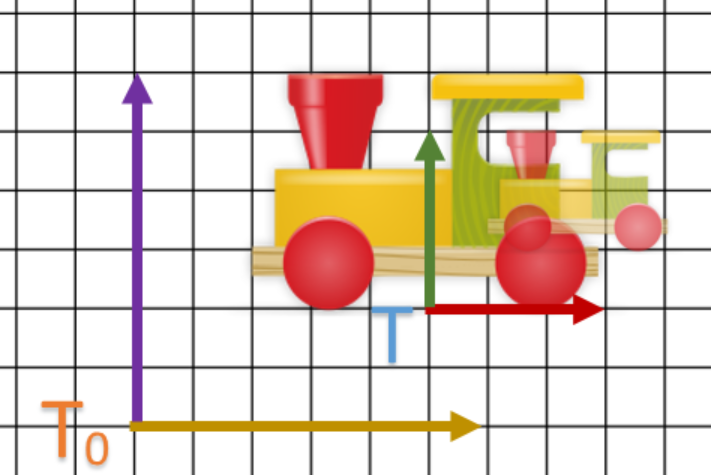
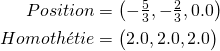
Le personnage
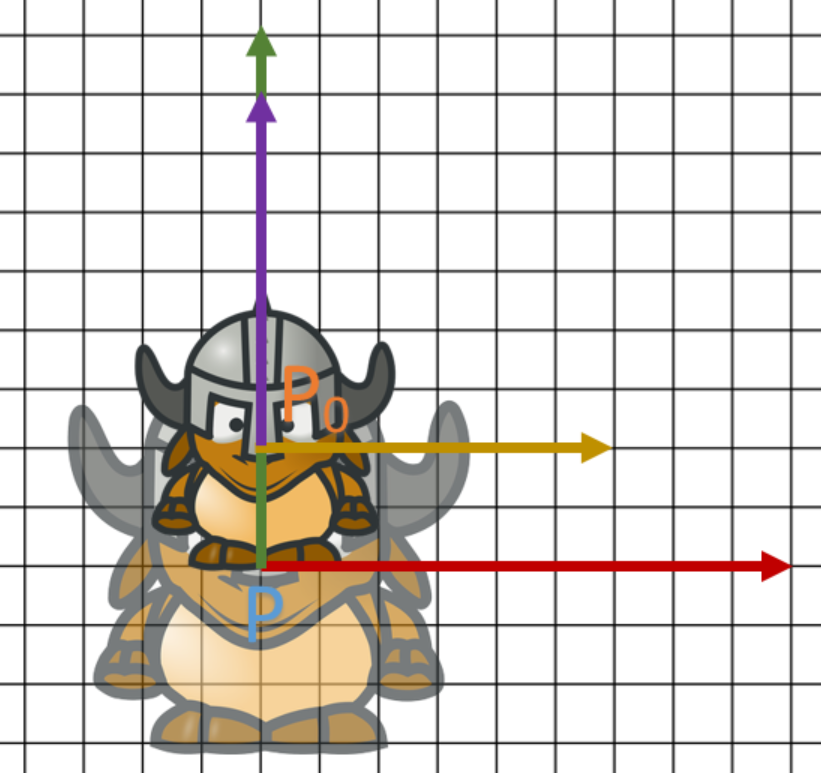
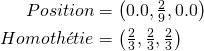
A ce stade, on a:
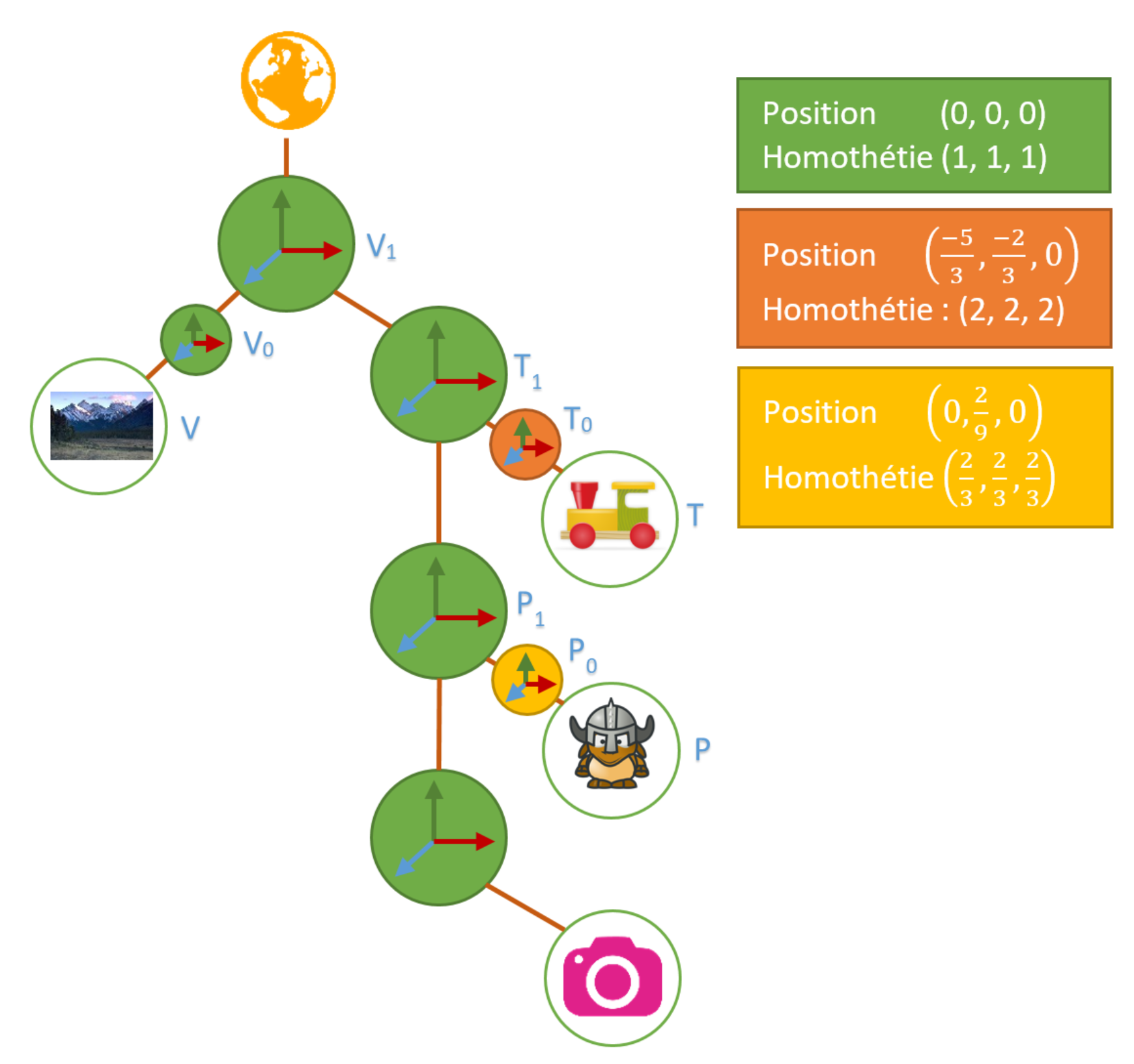
Il nous reste à calculer ![]() ,
, ![]() , on laissera l’identité à
, on laissera l’identité à ![]() .
.
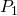 dans
dans 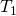
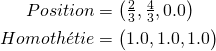
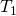 dans
dans 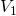
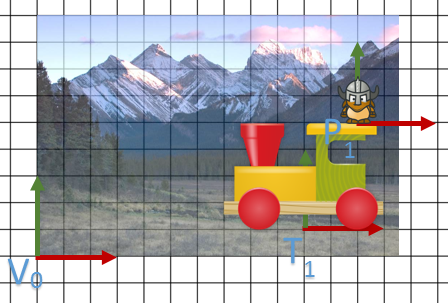
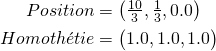
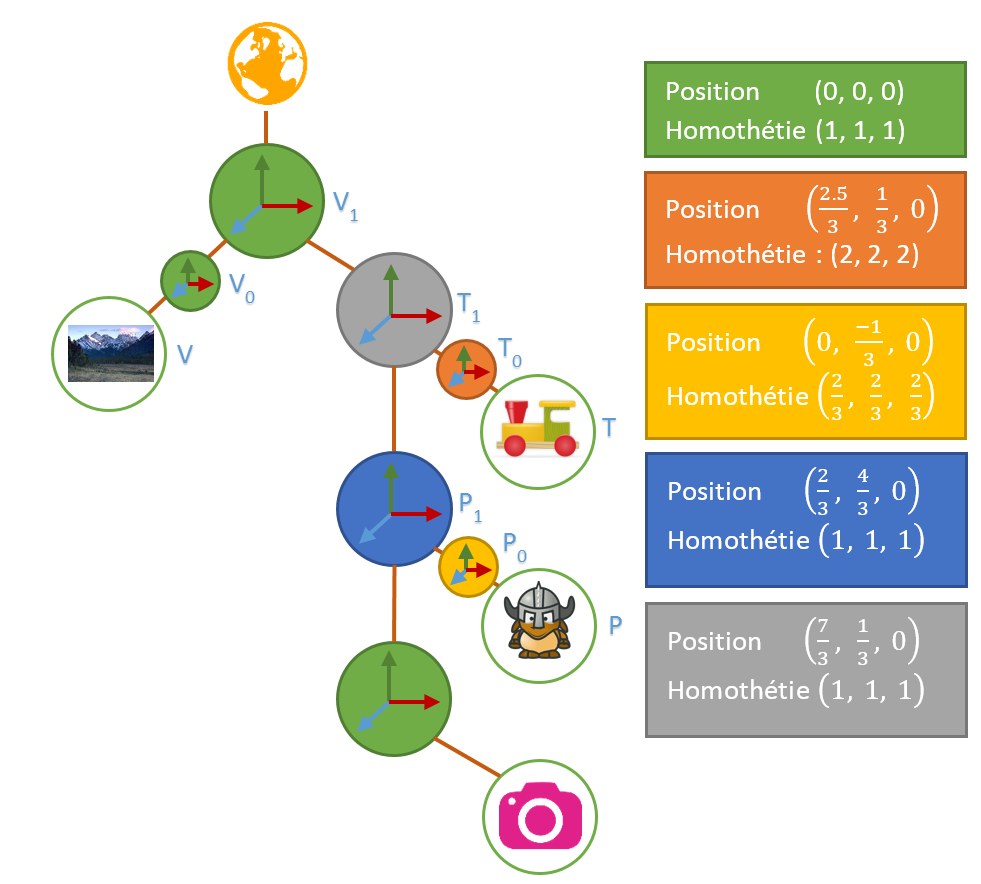
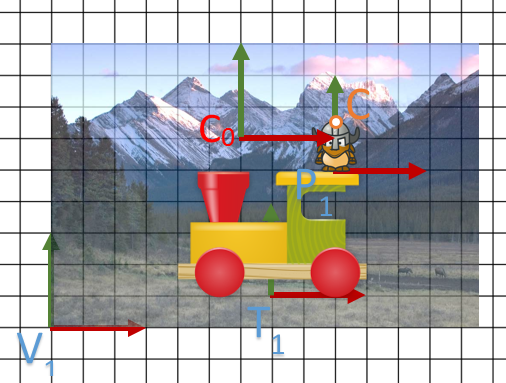
Finalement, on a notre scène finale.
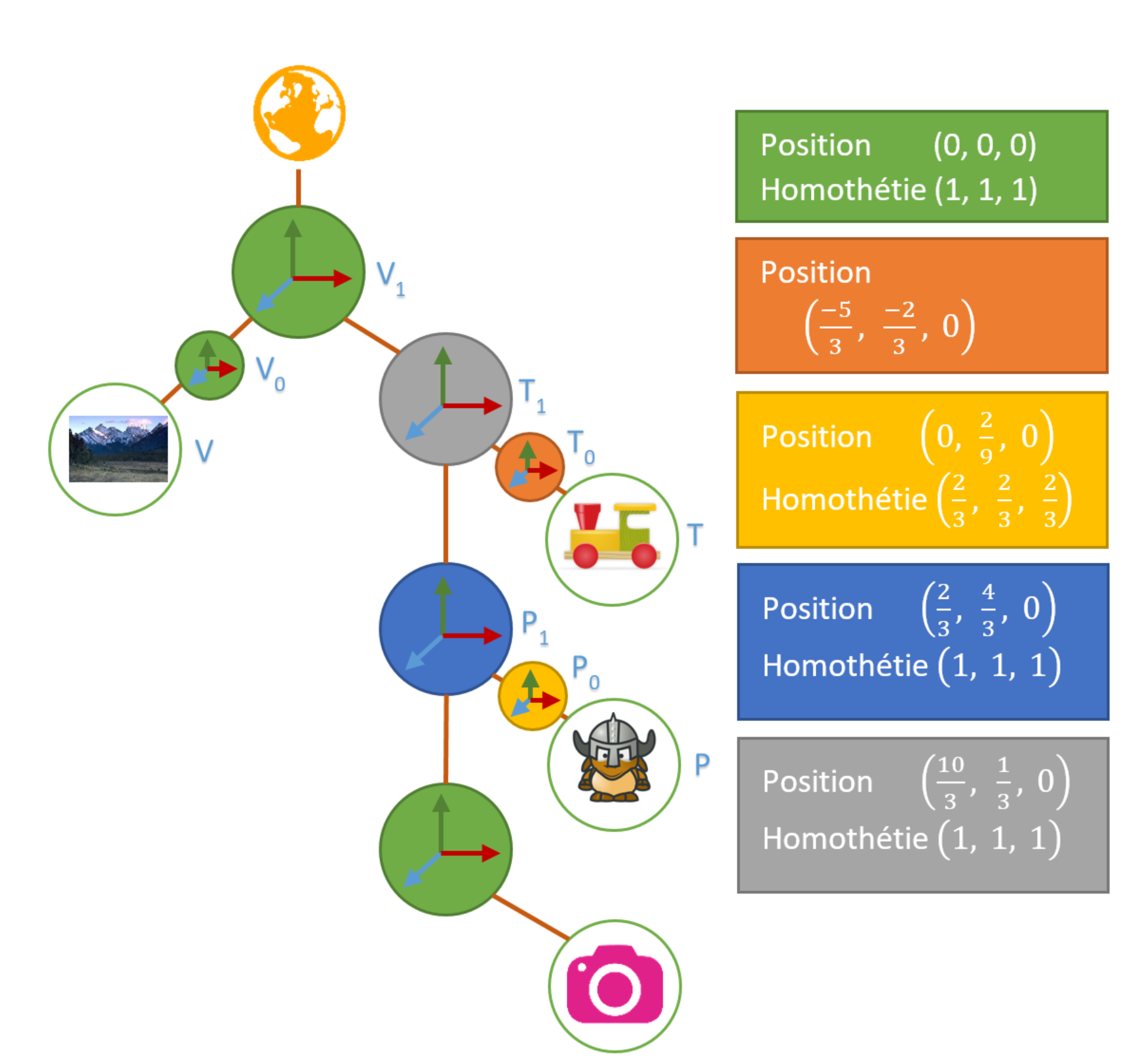
Bien évidemment, les infos positions/ homothéties sont calculées pour le sens “local vers monde”.
Voici leur écriture en c++/glm ainsi que la structure vue au chapitre précédent:
Transformation P0(glm::vec3(0.0f, 2.0f/9.0f, 0.0f), glm::vec3(2.0f/3.0f)); glm::mat4 P0(glm::scale(glm::translate(glm::mat4(1.0f), glm::vec3(0.0f, 2.0f/9.0f, 0.0f)), glm::vec3(2.0f/3.0f) ));
Au niveau code, on va définir deux classes scènes : une avec les matrices 4×4 et l’autre notre structure Transformation.
class SceneGraphTransformation
{
public:
SceneGraphTransformation() :
P0( glm::vec3( 0.0f, 2.0f/9.0f, 0.0f ), glm::vec3( 2.0f/3.0f ) ),
P1( glm::vec3( 2.0f/3.0f, 4.0f/3.0f, 0.0f ) ),
T0( glm::vec3( -5.0f/3.0f, -2.0f/3.0f, 0.0f ), glm::vec3( 2.0f ) ),
T1( glm::vec3( 10.0f/3.0f, 1.0f/3.0f, 0.0f ) ),
V1(),
C0( glm::vec3( -1.0f, 1.0f/3.0f, 0.0f ) )
{}
Transformation P0, P1, T0, T1, V1, C0;
};
class SceneGraphMatrix
{
public:
SceneGraphMatrix() :
P0( glm::scale( glm::translate( glm::mat4( 1.0f ), glm::vec3( 0.0f, 2.0f/9.0f, 0.0f ) ), glm::vec3( 2.0f/3.0f ) ) ),
P1( glm::translate( glm::mat4( 1.0f ), glm::vec3( 2.0f/3.0f, 4.0f/3.0f, 0.0f ) ) ),
T0( glm::scale( glm::translate( glm::mat4( 1.0f ), glm::vec3( -5.0f/3.0f, -2.0f/3.0f, 0.0f ) ), glm::vec3( 2.0f ) ) ),
T1( glm::translate( glm::mat4( 1.0f ), glm::vec3( 10.0f/3.0f, 1.0f/3.0f, 0.0f ) ) ),
V1( glm::mat4( 1.0f ) ),
C0( glm::translate( glm::mat4( 1.0f ), glm::vec3( -1.0f, 1.0f/3.0f, 0.0f ) ) )
{}
glm::mat4 P0, P1, T0, T1, V1, C0;
};
Calculons
Nous allons commencer à faire quelques calculs simples sur notre graphe afin de vérifier que tout marche bien.
Où est mon point ?
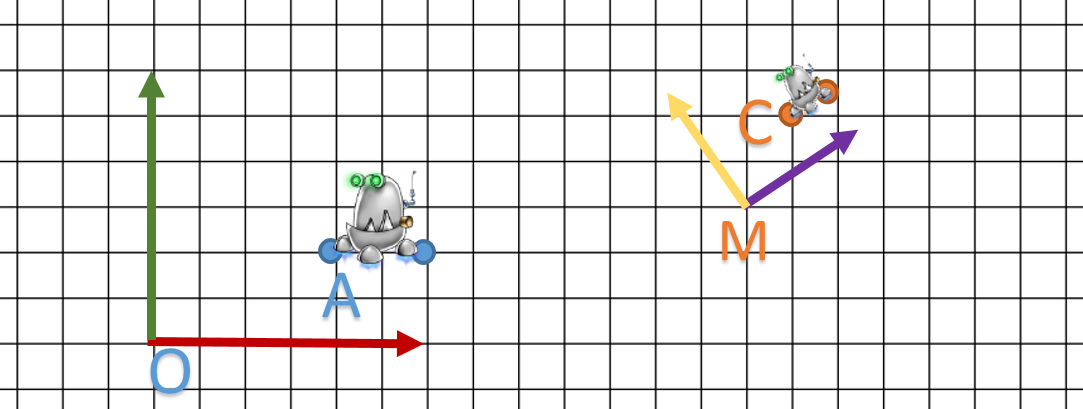
Soit C un point du casque de notre personnage défini par ![]() dans le repère P.
dans le repère P.
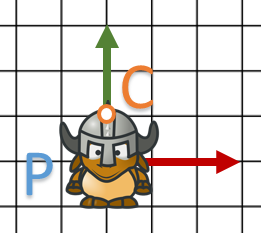
On va chercher à calculer où se trouve C dans V1.
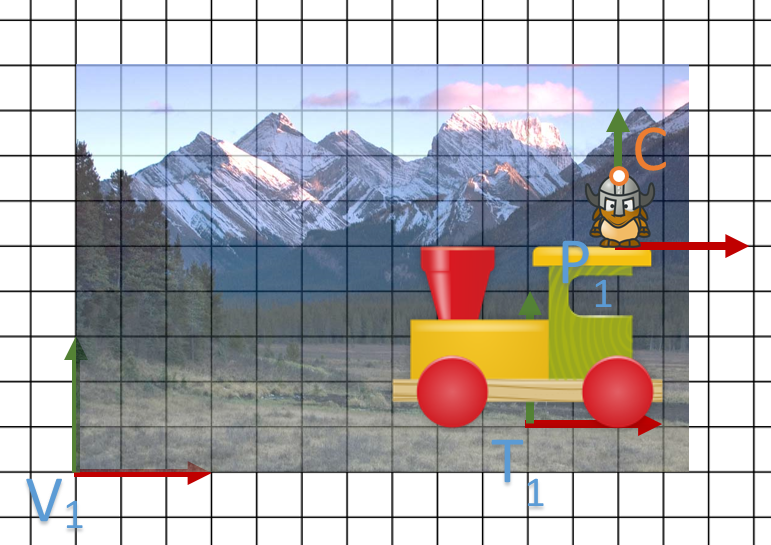
L’objectif ici est simple: composer toutes les transformations dans le bon ordre et multiplier C par celle-ci; soit le travail suivant:
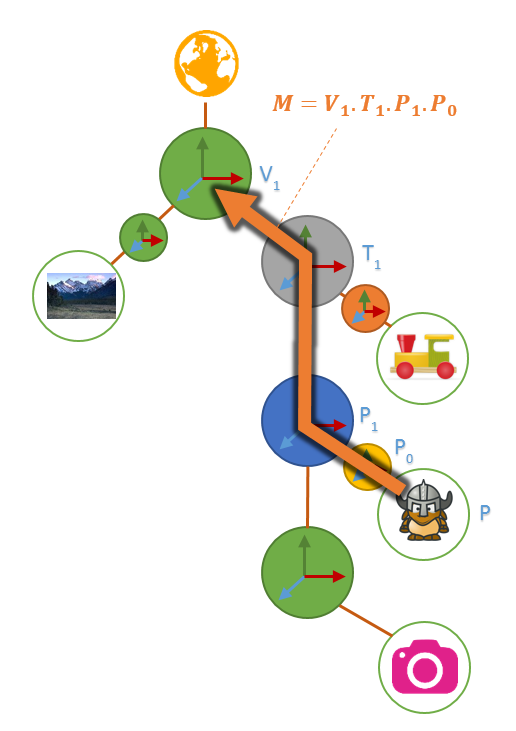
const float precision = 1e-5f; const SceneGraphTransformation scene; // Compute composed transformation and apply to C. const glm::vec3 C(0.0f, 1.0f/3.0f, 0.0f); const Transformation model = scene.V1 * (scene.T1 * (scene.P1 * scene.P0)); const glm::vec3 CinW = model * C; EXPECT_VEC3_NEAR(glm::vec3(4.0f, 19.0f/9.0f, 0.0f), CinW, precision);
const float precision = 1e-5f; const SceneGraphMatrix scene; // Compute composed matrix and apply to C. const glm::vec4 C(0.0f, 1.0f/3.0f, 0.0f, 1.0f); const glm::mat4 model = scene.V1 * (scene.T1 * (scene.P1 * scene.P0)); const glm::vec4 CinW = model * C; EXPECT_VEC4_NEAR(glm::vec4(4.0f, 19.0f/9.0f, 0.0f, 1.0f), CinW, precision);
Conclusion
- On a bien notre résultat attendu.
- Ici les transformations calculées précédemment sont dans le bon sens donc il n’y a rien de plus à faire que les écrire en C++.
- On se méfiera des parenthèses lors du calcul de la composée !
Au niveau littérature, ![]() ou
ou ![]() ou
ou ![]() , … se nomme une matrice modèle (ou Model Matrix en anglais).
, … se nomme une matrice modèle (ou Model Matrix en anglais).
Ce terme ne me plait pas à cause du mot “Matrix”. Avec la structure Transformation, on calcule la même chose et ce n’est pas une matrice … Je pense que c’est historique car OpenGL ne manipule que des matrices depuis sa création.
Je préfère qu’on parle transformation modèle et transformation modèle-monde, la composée qui part d’un objet (affichable) et qui remonte jusqu’au nœud monde.
Ces termes sont discutables.
Utilité des nœuds Transformations
Pour le moment, on n’a jamais vraiment remis en question le graphe de scène originel que je vous ai donné en début d’article.
En effet, on pourrait supprimer tous les nœuds transformations : les identités (nœud en vert) ne servent pas et le positionnement de nos objets pourrait directement être fait en modifiant la valeur de nos points. On aurait donc le même résultat visuel sans calcul.
Alors la question est pourquoi les garde-t-on ?
Les deux utilités principales sont :
- Le partage d’un même maillage à divers endroit de la scène. On va donc utiliser un seul maillage (économie de mémoire, si notre objet fait 3 Mo de données maillage dupliqué 1024 fois on va vite remplir la carte graphique)
- La transformation collective des maillages.
On va donc étudier le deuxième point:
On va reprendre notre scène mais en bougeant la transformation ![]() . On va juste changer sa valeur de position comme suit:
. On va juste changer sa valeur de position comme suit:
Maintenant, on va calculer comme précédemment la composée de notre personnage et l’appliqué à C. Et voici le résultat:
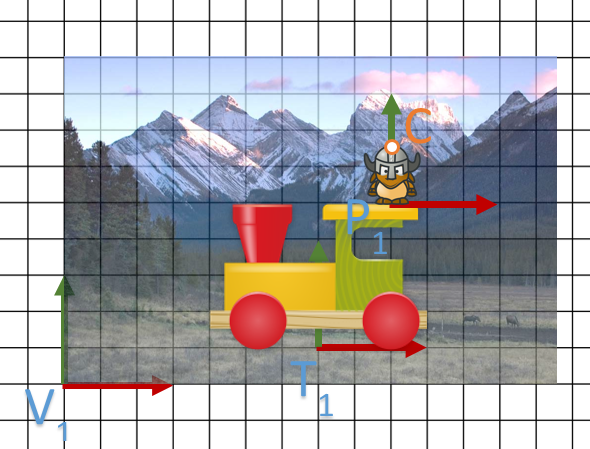
const float precision = 1e-5f; SceneGraphTransformation scene; // Move T1 to example position scene.T1 = Transformation( glm::vec3( 7.0f/3.0f, 1.0f/3.0f, 0.0f ) ); const glm::vec3 C( 0.0f, 1.0f/3.0f, 0.0f ); // Compose model const Transformation model = scene.V1 * (scene.T1 * (scene.P1 * scene.P0)); // Apply Model-view on C const glm::vec3 CinW = model * C; EXPECT_VEC3_NEAR( glm::vec3( 3.0f, 19.0f/9.0f, 0.0f ), CinW, precision );
Modèle-vue-projection
La modèle-vue-projection (ou modelview projection en anglais) est la matrice calculée et envoyée à nos systèmes de rendu (shader).
Elle se décompose en deux parties:
– Modèle-Vue : qui se lit modèle → vue.
– Projection : La matrice de projection 3D vers 2D (perspective ou orthogonale), on n’en parlera pas ici.
Le calcul de la modèle-vue se fait par la méthode suivante:
Composition des transformations:
-
-
- On part du modèle et on remonte jusqu’au monde
- On part du monde et on descend jusqu’à la camera de rendu: on appelle la
-
Pour la vue, on va calculer le chemin ci-dessous. Vu qu’on change de sens, il faudra inverser nos transformations.
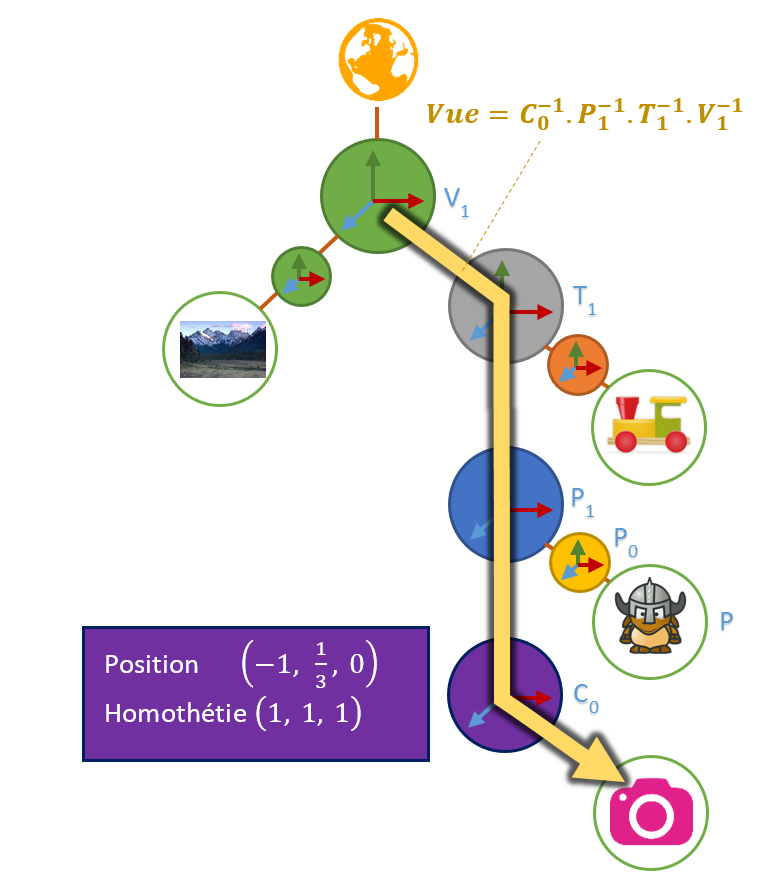
En composant, Modèle et Vue, on obtient le chemin complet qui permet d’exprimer les points d’un maillage dans le repère camera : la transformation modèle-vue (ou modelview en anglais).
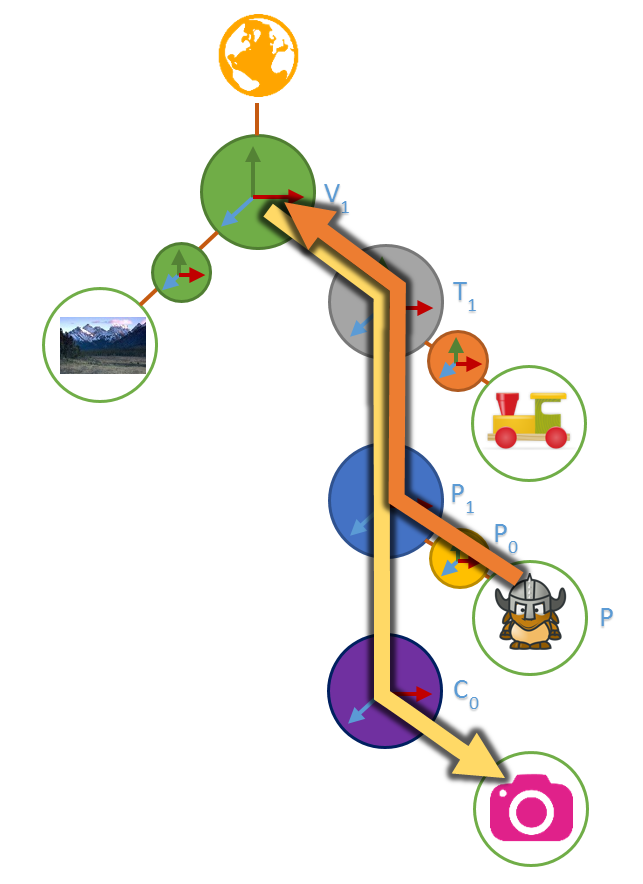
On va calculer C avec cette nouvelle transformation:
const float precision = 1e-5f;
SceneGraphTransformation scene;
// Move T1 to example position
scene.T1 = Transformation( glm::vec3( 8.0f/3.0f, 1.0f/3.0f, 0.0f ) );
const glm::vec3 C( 0.0f, 1.0f/3.0f, 0.0f );
// Compose model
const Transformation model = scene.V1 * (scene.T1 * (scene.P1 * scene.P0));
// Compose view
const Transformation view =
(Transformation::inverse(scene.C0) * (Transformation::inverse(scene.P1) *
(Transformation::inverse(scene.T1) * Transformation::inverse(scene.V1))));
// Apply Model-view on C
const glm::vec3 CinCamera = view * (model * C);
// Test it !
EXPECT_VEC3_NEAR( glm::vec3( 1.0f, 1.0f/9.0f, 0.0f ), CinCamera, precision );
// Another way is to compute "model orientation" of camera and inverse at the end !
const Transformation viewAlternative =
Transformation::inverse( scene.V1 * (scene.T1 * (scene.P1 * scene.C0)) );
EXPECT_VEC3_NEAR( viewAlternative._position, view._position, precision );
EXPECT_VEC3_NEAR( viewAlternative._homothetie, view._homothetie, precision );
Au final, notre scène est opérationnelle, il nous restera donc à calculer chacune des modèle-vue et de les transmettre à notre système de rendu (shaders, matrice OpenGL, …).
Utilisation dans un shader
Voici un exemple de shader extrait de l’excellent GitHub pour apprendre Vulkan: GitHub SaschaWillems
Ici on retrouve dans la structure uniform UBO les données précédemment vues ainsi que l’utilisation (conversion du point maillage) gl_Position = ubo.projection * ubo.view * ubo.model * tmpPos;.
#version 450
layout (location = 0) in vec4 inPos;
layout (location = 1) in vec2 inUV;
layout (location = 2) in vec3 inColor;
layout (location = 3) in vec3 inNormal;
layout (location = 4) in vec3 inTangent;
layout (binding = 0) uniform UBO
{
mat4 projection;
mat4 model;
mat4 view;
vec4 instancePos[3];
} ubo;
layout (location = 0) out vec3 outNormal;
layout (location = 1) out vec2 outUV;
layout (location = 2) out vec3 outColor;
layout (location = 3) out vec3 outWorldPos;
layout (location = 4) out vec3 outTangent;
out gl_PerVertex
{
vec4 gl_Position;
};
void main()
{
vec4 tmpPos = inPos + ubo.instancePos[gl_InstanceIndex];
gl_Position = ubo.projection * ubo.view * ubo.model * tmpPos;
outUV = inUV;
outUV.t = 1.0 - outUV.t;
// Vertex position in world space
outWorldPos = vec3(ubo.model * tmpPos);
// GL to Vulkan coord space
outWorldPos.y = -outWorldPos.y;
// Normal in world space
mat3 mNormal = transpose(inverse(mat3(ubo.model)));
outNormal = mNormal * normalize(inNormal);
outTangent = mNormal * normalize(inTangent);
// Currently just vertex color
outColor = inColor;
}
Conclusion
Au fil de cette série d’article, on a vu comment manipuler et former des transformations basées sur les matrices 4×4 ou les quaternions et on a utilisé tout ça afin de former un graphe de scène. Il ne nous reste maintenant qu’à exploiter ces données dans un système de rendu (Qt, OpenGL, Vulkan, DirectX, …).
La hiérarchie des nœuds de transformation est extrêmement utile car en bougeant le nœud de haut niveau, on déplace tous ceux qui en dépendent.
Par exemple, j’ai une scène avec une table sur laquelle se trouve des objets (lampe, mug, …); si je déplace la table, mes objets vont rester à la même position sur la table.
Pensez toujours à faire des graphes de scène simple. D’ailleurs, la critique qu’on pourrait faire de celui que je vous ai présenté est bien sur les nœuds ![]() ,
, ![]() ,
, ![]() .
.
Ici ils n’apportent rien, le plus simple serait de modifier les points du maillage directement.
J’espère que ce type de série vous a plu. Ça va me permettre de poser les bases du rendu 3D et ainsi aller plus loin dans les futurs articles.
Merci d’avoir lu cet article !
N’hésitez pas à le partager, à me signaler les problèmes, et aussi à le commenter afin d’en faire un outils dynamique et constructif !
Sources
OpenGL Tutorial: Les matrices
Matrices dans OpenGL 4
Introduction to Scene Graphs
Viewing and Modeling