Matrice, Quaternion et graphe de scène – Partie 2
Nous allons parler dans cette article de quaternion et des opérations qu’on peut faire avec mais surtout de comment remplacer nos matrices de transformation par une structure utilisant les quaternions.
Cet article s’inscrit dans une suite :
- Matrice, Quaternion et graphe de scène – Partie 1
- Matrice, Quaternion et graphe de scène – Partie 2
- Matrice, Quaternion et graphe de scène – Partie 3
Tous les exemples sont sur mon GitHub https://github.com/Rominitch/myBlogSource/ dans Matrix_Quaternion.
Les quaternions
Pré-ambule
Avant de commencer, je vais poser quelques nouvelles notations pour clarifier les futures formules mathématiques.
 est la multiplication d’un quaternion avec un point/vecteur.
est la multiplication d’un quaternion avec un point/vecteur. est la multiplication d’un point/vecteur par un ou des scalaires (composante par composante).
est la multiplication d’un point/vecteur par un ou des scalaires (composante par composante).
Définition
Les quaternions permettent d’exprimer une rotation 3D en utilisant uniquement quatre composantes (en passant par un espace 4D).
La représentation la plus facile à comprendre est la suivante:
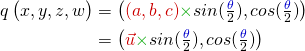
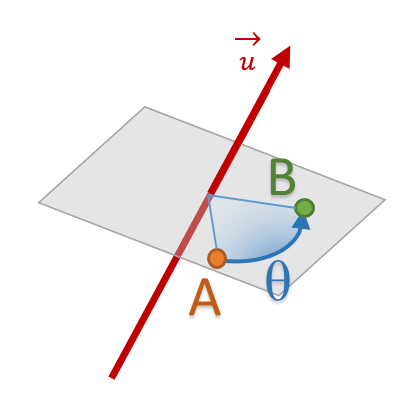
Voici une démo en ligne pour comprendre rapidement comment s’opère la rotation: Quaternions Online
Les opérations les plus importantes pour nous sont:
- la multiplication (avec des quaternions et des vecteurs)
- l’inversion
- l’interpolation slerp (dans un deuxième temps)
Comme précédemment, je considère que vous savez les faire (sinon glm le fera pour vous).
A ce stade, les quaternions sont juste un autre moyen d’exprimer une rotation (comme les angles d’Euler et les matrices 3×3).
Une première question nous vient: Pourquoi donc les utiliser ?
La réponse est la suivante:
- Peu de composantes et opération simple donc très rapide à calculer sur nos ordinateurs.
- Interpolation facile (très utile pour les animations).
Matrice et Quaternion
De notre point de vue, les quaternions permettent de remplacer la matrice de rotation uniquement.
Donc là où une matrice homogène contenait toutes les infos, il faudra inventer un outils permettant de combiner notre quaternion, le facteur d’agrandissement et la position de notre repère en plus : la structure Transformation.
struct Transformation
{
glm::vec3 _homothetie;
glm::quat _rotation;
glm::vec3 _position;
}
Dans la littérature américaine (et les codes sources), on parle de classe/structure “Transform”.
Opérations sur notre structure
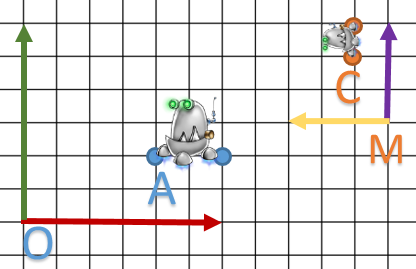
La première chose est de calculer la multiplication de notre structure avec un point afin d’appliquer toutes les transformations.
On va partir de cet exemple: ![]() un point de l’objet, on souhaite appliquer une rotation de
un point de l’objet, on souhaite appliquer une rotation de ![]() , une homothétie de
, une homothétie de ![]() et
et ![]() exprimé dans O.
exprimé dans O.
Ce qui va nous donner le point ![]()
Multiplication
On trouve sur les forums des gens qui convertissent leur structure en matrice homogène qui composent les matrices et recréer leur structure.
Ici, ils n’utilisent pas les opérateurs des quaternions ! Ne tomber pas dans le piège.
Notre premier but est de créer un opérateur de multiplication qui comme pour les matrices va nous transformer les coordonnées de notre point du repère local vers le repère monde.
Comme pour les compositions des matrices, on va multiplier notre point dans l’ordre: ![]()
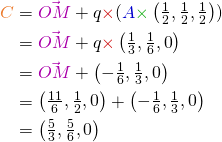
glm::vec3 Transformation::multiplierVersMonde(const glm::vec3& point) const
{
return _position + _rotation * (point * _homothetie);
}
glm::vec3 Transformation::operator * (const glm::vec3& localPoint) const
{
return multiplierVersMonde(localPoint);
}
glm::vec4 a( 4.0f/6.0f, 2.0f/6.0f, 0.0f, 1.0f );
glm::vec4 c( 10.0f/6.0f, 5.0f/6.0f, 0.0f, 1.0f );
Transformation qc;
qc._homothetie = glm::vec3( 0.5f, 0.5f, 0.5f );
qc._rotation = glm::angleAxis( PI * 0.5f, glm::vec3( 0.0f, 0.0f, 1.0f ) );
qc._position = glm::vec3(11.0f/6.0f, 0.5f, 0.0f );
glm::vec3 cal_c = qc * a;
EXPECT_VEC3_NEAR( c, cal_c, precision );
Comme pour les matrices, la multiplication n’est pas commutative.
glm a défini pour nous les deux sens de la multiplication: ne nous trompons pas de sens !
Voici un petit exemple:
const float angle = PI * 0.5f; glm::quat q = glm::angleAxis( angle, glm::vec3( 0.0f, 0.0f, 1.0f ) ); glm::vec4 a( 1.0f, 1.0f, 0.0f, 1.0f ); glm::vec4 c( -1.0f, 1.0f, 0.0f, 1.0f ); glm::vec3 cal_c = q * a; EXPECT_VEC3_NEAR( c, cal_c, precision ); glm::vec3 cal_a = c * q; EXPECT_VEC3_NEAR( a, cal_a, precision );
L’inversion
L’inversion de notre structure est possible car chaque élément la constituant est inversible.
La seule difficulté ici est de trouver la nouvelle translation (qui n’est pas juste le vecteur opposé). On prend notre vecteur ![]() qu’on doit lire dans le repère M: on va écrire ça
qu’on doit lire dans le repère M: on va écrire ça ![]() .
.
Donc on lui applique l’inverse de l’homothétie et l’inverse de la rotation (dans cet ordre).
Dans le cas particulier où l’on n’a ni rotation, ni homothétie, on a bien comme solution ![]() .
.
On va avoir l’opérateur suivant:
void Transformation::inverse()
{
_homothetie = 1.0f / _homothetie;
_rotation = glm::inverse( _rotation );
_position = -(_rotation * (_homothetie * _position));
}
On va donc calculer et tester l’inversion de notre structure en partant de C vers A.
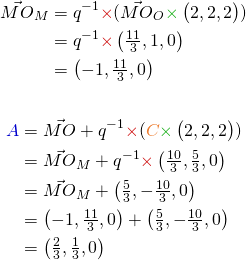
const float angle = PI * 0.5f; glm::vec3 om( 11.0f/6.0f, 0.5f, 0.0f ); glm::vec3 homothetie( 0.5f, 0.5f, 0.5f ); glm::vec4 a( 4.0f/6.0f, 2.0f/6.0f, 0.0f, 1.0f ); glm::vec4 c( 10.0f/6.0f, 5.0f/6.0f, 0.0f, 1.0f ); Transformation qc; qc._homothetie = homothetie; qc._rotation = glm::angleAxis( angle, glm::vec3( 0.0f, 0.0f, 1.0f ) ); qc._position = om; Transformation qa(qc); qa.inverse(); glm::vec3 cal_c = qc * a; EXPECT_VEC3_NEAR( c, cal_c, precision ); glm::vec3 cal_a = qa * c; EXPECT_VEC3_NEAR( a, cal_a, precision );
Composition de notre structure
Maintenant nous allons composé notre structure. Pour commencer, on va prendre un cas simple : comme avec les matrices, on va composer une structure d’homothétie, une autre de rotation et finalement la dernière de translation. Dans ce cas, on va générer des éléments neutres (soit en addition ou multiplication).
Voici la solution finale
// World = This * Local
Transformation operator * ( const Transformation& localSpace ) const
{
Transformation worldSpace;
worldSpace._homothetie = _homothetie * localSpace._homothetie;
worldSpace._rotation = _rotation * localSpace._rotation;
worldSpace._position = _position + _rotation
* (localSpace._position * _homothetie);
return worldSpace;
}
glm::vec3 homothetie( 0.5f, 0.5f, 0.5f );
float angle = PI / 2.0f;
glm::vec3 axis( 0.0f, 0.0f, 1.0f );
glm::vec3 pos( 11.0f/6.0f, 0.5f, 0.0f );
glm::vec4 a( 2.0f/3.0f, 1.0f/3.0f, 0.0f, 1.0f );
glm::vec4 c( 5.0f/3.0f, 5.0f/6.0f, 0.0f, 1.0f );
Transformation s;
s._homothetie = homothetie;
Transformation r;
r._rotation = glm::angleAxis( angle, axis );
Transformation t;
t._position = pos;
Transformation qc = t * (r * s);
// Near except
glm::vec3 cal_c = qc * a;
EXPECT_VEC3_NEAR( c, cal_c, precision );
Donc il ne nous reste plus qu’à tester tout ça sur un exemple complexe.
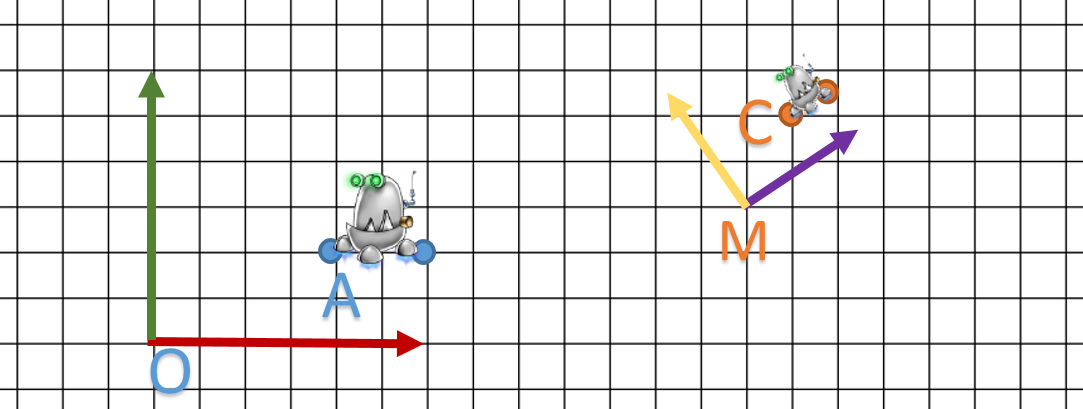
Soit le schéma suivant avec le repère O, M et R qui sont hiérarchisés de la manière suivante O → M → R. On pose ![]() comme le point
comme le point ![]() défini dans R avec les coordonnées
défini dans R avec les coordonnées ![]() et on cherche les coordonnées de C défini dans le repère O soit
et on cherche les coordonnées de C défini dans le repère O soit ![]() .
.
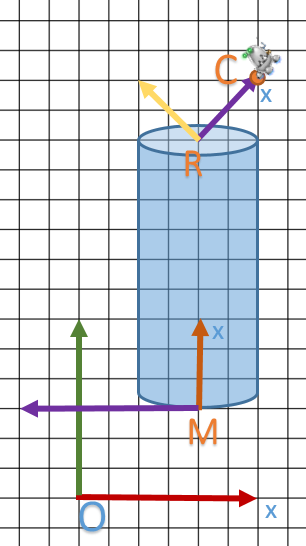
On va définir la structure de M 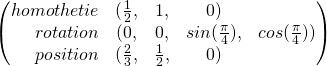 et R
et R 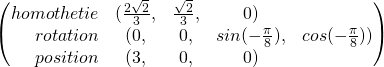 .
.
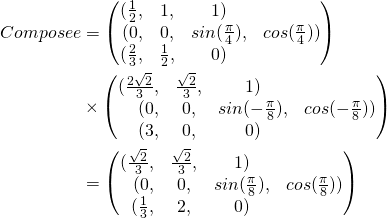
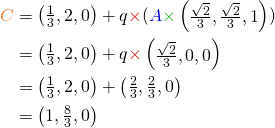
float angleM = PI / 2.0f;
float angleR = -PI / 4.0f;
const glm::vec3 axis( 0.0f, 0.0f, 1.0f );
const glm::vec4 a( 1.0f, 0.0f, 0.0f, 1.0f );
const glm::vec4 c( 1.0f, 7.0f/3.0f, 0.0f, 1.0f );
Transformation qm;
qm._homothetie = glm::vec3( 0.5f, 1.0f, 1.0f );
qm._rotation = glm::angleAxis( angleM, axis );
qm._position = glm::vec3(2.0f/3.0f, 1.0f/2.0f, 0.0f);
Transformation qr;
qr._homothetie = glm::vec3( sqrt_2 * 2.0f/3.0f, sqrt_2 / 3.0f, 1.0f );
qr._rotation = glm::angleAxis( angleR, axis );
qr._position = glm::vec3(3.0f, 0.0f, 0.0f);
EXPECT_VEC3_NEAR( glm::vec3(2.0f/3.0f, 2.0f, 0.0f),
qm * qr._position, precision );
// Composition
Transformation qc = qm * qr;
// Near except
glm::vec3 cal_c = qc * a;
EXPECT_VEC3_NEAR( c, cal_c, precision );
Enfin !!! A ce stade, nos matrices homogènes et notre structure avec quaternion font exactement la même chose.
Avant de passer à la dernière partie, je souhaiterai vous monter un avantage supplémentaire avec l’interpolation.
Interpolation
Dans ce dernier chapitre, nous allons donc interpoler notre structure. Il existe deux types d’interpolation des quaternions soit linéaire (lerp) ou sphérique (slerp)
On va créer donc deux fonctions ou seul l’interpolation du quaternion change (l’homothétie et la position seront interpolées linéairement).
static Transformation lerp(const Transformation& a, const Transformation& b, const float factor)
{
Transformation interpole;
interpole._homothetie = a._homothetie + (b._homothetie - a._homothetie) * factor;
interpole._rotation = glm::lerp( a._rotation, b._rotation, factor );
interpole._position = a._position + (b._position - a._position) * factor;
return interpole;
}
static Transformation slerp( const Transformation& a, const Transformation& b, const float factor )
{
Transformation interpole;
interpole._homothetie = a._homothetie + (b._homothetie - a._homothetie) * factor;
interpole._rotation = glm::slerp( a._rotation, b._rotation, factor );
interpole._position = a._position + (b._position - a._position) * factor;
return interpole;
}
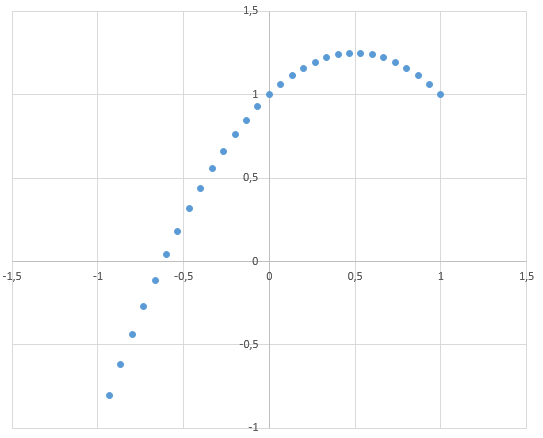
Nous allons prendre un petit exemple : on va prendre un point ![]() et on va le multiplier par notre structure interpolé à différent moment de l’interpolation.
et on va le multiplier par notre structure interpolé à différent moment de l’interpolation.
On va partir du repère classique (pas de rotation, position O et pas d’homothétie). Et on va aller vers une rotation de 180 degrés (ou PI).
Voici le programme et sa courbe pour les deux modes d’interpolation.
float angle = PI;
const glm::vec3 axis( 0.0f, 0.0f, 1.0f );
const glm::vec4 a( 1.0f, 1.0f, 0.0f, 1.0f );
// World
Transformation qo;
// Rotation de 180 degrés
Transformation qm;
qm._rotation = glm::angleAxis( angle, axis );
const int animation = 30;
for( int i=0; i < animation; ++i)
{
float f = float( i ) / float( animation - 1 );
Transformation qc = Transformation::lerp( qo, qm, f );
// Near except
glm::vec3 cal_c = qc * a;
std::cout << cal_c.x << " " << cal_c.y << std::endl;
}
float angle = PI;
const glm::vec3 axis( 0.0f, 0.0f, 1.0f );
const glm::vec4 a( 1.0f, 1.0f, 0.0f, 1.0f );
// World
Transformation qo;
// Rotation de 180 degrés
Transformation qm;
qm._rotation = glm::angleAxis( angle, axis );
const int animation = 30;
for( int i=0; i < animation; ++i)
{
float f = float( i ) / float( animation - 1 );
Transformation qc = Transformation::slerp( qo, qm, f );
// Near except
glm::vec3 cal_c = qc * a;
std::cout << cal_c.x << " " << cal_c.y << std::endl;
}
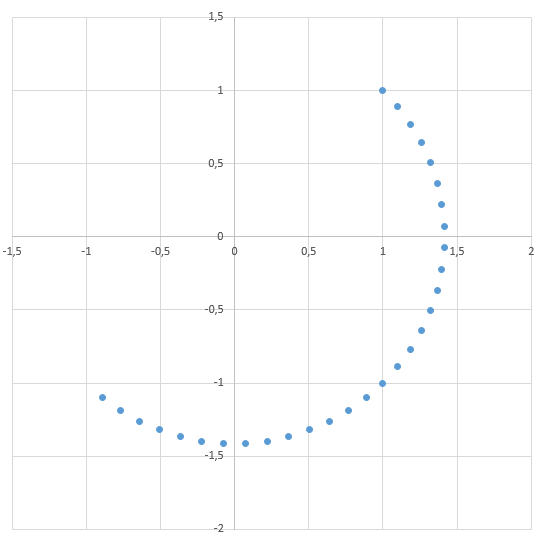
Et voici finalement un cas complet d’interpolation entre deux structures.
float angle = PI;
const glm::vec3 axis( 0.0f, 0.0f, 1.0f );
const glm::vec4 a( 1.0f, 1.0f, 0.0f, 1.0f );
Transformation qo;
Transformation qm;
qm._homothetie = glm::vec3( 2.0f, 2.0f, 2.0f );
qm._rotation = glm::angleAxis( angle, axis );
qm._position = glm::vec3(4.0f, 4.0f, 0.0f);
const int animation = 30;
for( int i=0; i < animation; ++i)
{
float f = float( i ) / float( animation - 1 );
Transformation qc = Transformation::slerp( qo, qm, f );
// Near except
glm::vec3 cal_c = qc * a;
std::cout << cal_c.x << "," << cal_c.y << std::endl;
}
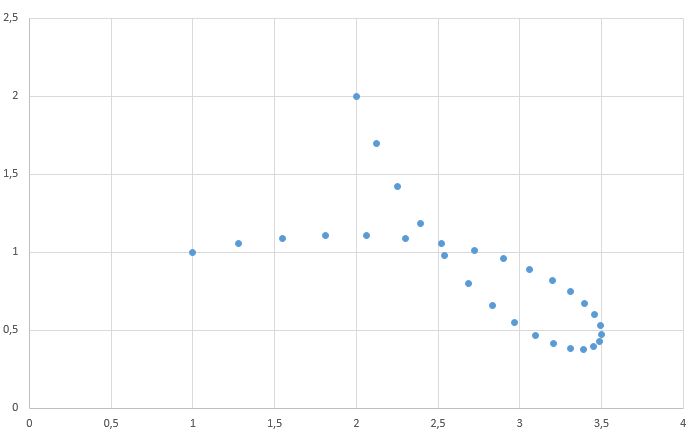
Conclusion
Comme nous l’avons vu, les quaternions ne sont que la représentation d’une rotation dans l’espace. Les matrices homogènes possèdent deux informations supplémentaires : l’homothétie et la translation. On a donc créé une structure permettant de compléter ce manque et rajouter les opérateurs pour avoir un équivalent aux matrices homogènes.
Il ne nous reste plus qu’à utiliser nos nouveaux jouets dans un cas concret : le graphe de scène.
Matrice, Quaternion et graphe de scène – Partie 3
Sources
ENS – Cours : Quaternions
IRIT – COURS : Quaternions
Geeks3D – How to rotate a vertex by a quaternion in glsl ?